An Efficient Algorithm for Determining the Composition Relationship of Polarized Morphisms

Wayne Peng

National Chung Hsing University

A taste of arithmetic dynamics

Let $f$ be a polynomial over integer, and let $a$ be an arbitrary integer. We call a prime $p$ a primitive prime of the sequence $\{f^n(a)\}$ if $p$ divides $f^m(a)$ for some $m$ and no further term before $m$ is divisible by $p$.

We call $a$ a preperiodic point of $f$ if $f^m(a)=f^n(a)$ for some distinct integer $m$ and $n$, and call it periodic point if $f^m(a)=a$ for some integer $m$.
We would like to know the size of $$\text{Prep}(f,\mathbb{Q})=\{a\in\mathbb{Q}\mid a\text{ is a preperiodic point of }f\}$$ and $$\text{Per}(f,\mathbb{Q})=\{a\in\mathbb{Q}\mid a\text{ is a periodic point of }f\}$$

Composition and Decomposition

Performing composition with rational functions $f$ and $g$ is straightforward. However, decomposing a function $F$ can be a challenging task. $$ \frac{x^2+1}{2x}\circ \frac{2x+1}{x^2-1}=\frac{5x^2+4x}{4x^3+x^2-4x-1}$$

  • trivial decomposition: a decomposition $F=F_1\circ F_2$ is trivial if $F_1$ or $F_2$ is a linear map.
  • indecomposible: we say a morphism $F$ is indecomposible if any decomposition of $F$ is trivial.

Ritt's Decomposition Theorem

We say $F=F_1\circ F_2\circ\cdots\circ F_n$ is a complete decomposition of $F$ if each $F_i$ is indecomoposible.

  1. Complete decomposition exists and is unique in some sense.
  2. For any two complete decompositions, $$ f_1^{d_1}\circ f_2^{d_2}\circ\cdots\circ f_n^{d_n} = g_1^{e_1}\circ g_2^{e_2}\circ\cdots\circ g_n^{e_n}. $$ we have an algorithm that can move from the left to the right in finitely many steps.

Lüroth's Theorem

Let $K$ be a field and $M$ be an intermediate field between $K$ and $K(X)$, for some transcendental element $X$ over $K$. Then there exists a rational function $f(X)\in K(X)$ such that $M=K(f(X))$. In other words, every intermediate extension between $K$ and $K(X)$ is a simple extension.

  • An effective version of Lüroth Theorem provides an algorithm for decomposing rational functions. Alonso, Gutierrez, and Recio published the first paper on this topic on JSC in 1995.
  • Higher dimensional cases remain unclear.

Composition Relation

We say two functions $f$ and $g$ have composition relation if there exist nontrivial solutions for $$ A_n\circ A_{n-1}\circ\cdots\circ A_1 = B_n\circ B_{n-1}\circ\cdots\circ B_1 $$ where $A_i$ and $B_i$ are either $f$ or $g$.

We say that $\langle f,\ g\rangle$ is a rank 2 free generated semigroup with composition as the operation if $f$ and $g$ have no compositional relation.

p.s. If we further consider the addition of functions, then we call the structure near ring.

Composition relation: commutativity

A rational map $f$ of degree two or more will be called a finite quotient of an affine map if there is a flat surface $\mathbb{C}/\Lambda$, an affine map $L(t) = at+b$ from $\mathbb{C}/\Lambda$ to itself, and a finite-to-one holomorphic map $\theta: \mathbb{C}/\Lambda \to \mathbb{C}\setminus \mathcal{E}_f$ which satisfies the semiconjugacy relation $f \circ \theta = \theta \circ L$, i.e. the following diagram commute:

Composition relation: odd function

Let $f(x)=x^3+x$ and $g(x)=-x^3-x$. We have $$ f\circ f = g\circ g. $$

Is there any $f$ and $g$ where their Julia sets are not the "same" and satisfy $$f\circ g\circ f=g\circ f\circ g?$$

Our Result

$h_f\neq h_g$ if and only if there exists an integer $j$ such that $\langle f^j,g^j\rangle$ is a rank 2 free generated semigroup.
The followings are equivalent:
  • $\text{Prep}(f)\cap\text{Prep}(g)$ is infinite;
  • $\text{Prep}(f)=\text{Prep}(g)$;
  • for any $w_1,w_2\in\langle f,g\rangle$, we have $\text{Prep}(w_1)=\text{Prep}(w_2)$;
  • $\langle f,g\rangle$ has polynomial growth;
  • $\langle f,g\rangle$ does not contain a nonabelian free semigroup;
  • for any $l>0$, the semigroup $\langle f^l,g^l\rangle$ is not a free semigroup on two generators.
  • $h_f=h_g$.

Height and Canonical Height

Let $\alpha=\frac{p}{q}\in\mathbb{Q}$ be a rational number in lowest terms. The naive height $h:\mathbb{Q}\to\mathbb{R}_{\geq 0}$ is $$ h(\alpha)=\log(\max\{|p|,|q|\}). $$

If we allow $\alpha$ not in lowest terms, the naive height is equivalent to $$ h(\alpha) = \sum_{p\in M_{\mathbb{Q}}} \log(\max\{1,|\alpha|_p\}) $$ where $M_{\mathbb{Q}}$ is the set of all places (absolute values) over $\mathbb{Q}$.

  • There exists a unique extension of height over any number field $K$.
  • It is possible to define a height function on any global field.
  • Our paper introduces a broader concept of height functions.
  • Let $f$ be a degree $d$ rational function. We have a constant $C_f$ such that the following inequality $$ |h(f(\alpha))-dh(\alpha)|\leq C_f $$ holds for any $\alpha\in K$. In other word, $h(f(\alpha))\sim dh(\alpha)$, so $h(f^n(\alpha))\sim d^nh(\alpha)$.

Suppose $d=\deg(f)>1$, and let $n>m>0$. We have $$ \begin{aligned} &\left|\dfrac{h(f^n(\alpha))}{d^n}-\dfrac{h(f^m(\alpha))}{d^m}\right|\\ &=\left|\dfrac{h(f^n(\alpha))}{d^n}-\dfrac{h(f^{n-1}(\alpha))}{d^{n-1}}\right.\\ &\left.+\dfrac{h(f^{n-1}(\alpha))}{d^{n-1}}-\cdots +\dfrac{h(f^{m+1}(\alpha))}{d^{m+1}}-\dfrac{h^m(\alpha)}{d^m}\right|\\ &\leq \dfrac{C_f}{d^n}+\dfrac{C_f}{d^{n-1}}+\cdots+\dfrac{C_f}{d^{m+1}} \end{aligned} $$

Therefore, the following limit, called canonical height, exists $$ h_f(\alpha) = \lim_{n\to\infty}\frac{h(f^n(\alpha))}{d^n}. $$

keys

Let $f$ and $g$ be rational functions of degrees greater than $1$. Let $\omega=\phi_m\cdots\phi_1$ where $\phi_j$ is equal to $f$ or $g$ for each $i$. Let $s_j=\phi_j\cdots \phi_1$ for $j\leq m$.

With the notation as above, we have $$ \left|\dfrac{h(w(\alpha))}{\deg\omega}-\dfrac{h(s_j(\alpha))}{\deg s_j}\right|<\dfrac{\max\{C_f,C_g\}}{\min\{\deg(f),\deg(g)\}^j} $$ for $j=1,\ldots,m$.

Prove a direction of our theorem

By the assumption, we choose an $\varepsilon< |h_f(\alpha)-h_g(\alpha)|/2\neq 0$. Then $B(h_f,\varepsilon)\cap B(h_g,\varepsilon)=\emptyset$.

By the previews lemma, we know there is a $j$ such that, for all words starting with $j$ many $f$, their canonical heights at $\alpha$ will stay in $B(h_f,\varepsilon)$.

Similarly, for all words starting with $j$ many $g$, their canonical heights at $\alpha$ will stay in $B(h_g,\varepsilon)$.

Thus we can conclude that any word starting with $j$ many $f$ won't equal to one starting with $j$ many $g$.

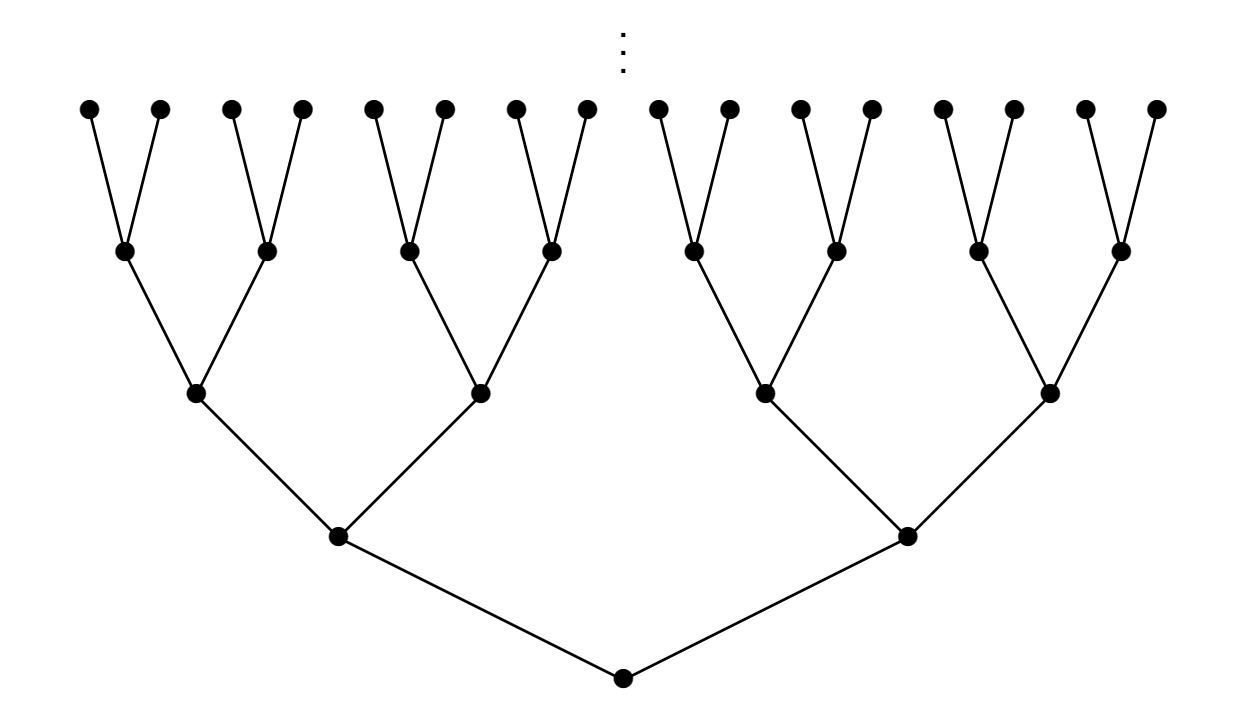
Algorithm

Input: polarized morphism $f$ and $g$, and an integer $n$

Output: A Boolean indicating whether $f$ and $g$ have a composition relation, or "indeterminable" if the algorithm cannot determine by the binary tree under level $n$.

Idea of Algorithm

  1. For simplicity, we assume $\deg f=\deg g$.
  2. Composition has right cancellation, i.e. $$ h_1\circ f = h_2\circ f\implies h_1=h_2. $$

    Therefore, to check if we have nontrivial composition relation, we can simply assume that the first (the most right) function is not the same.

  1. By previews lemma, if there exists some $\alpha$ such that $$ B\left(h\left(\dfrac{A(\alpha)}{d^n}\right),\dfrac{C}{(d-1)d^n}\right)\bigcap B\left(h\left(\dfrac{B(\alpha)}{d^n}\right),\dfrac{C}{(d-1)d^n}\right)=\emptyset $$ where $C=\max\{C_f, C_g\}$, $A=A_n\circ\cdots\circ A_1$ and $B=B_n\circ\cdots\circ B_1$, then any composition that starts with $A_n\circ\cdots\circ A_1$ won't be equal to one that starts with $B_n\circ\cdots\circ B_1$.

Datas and Discussion

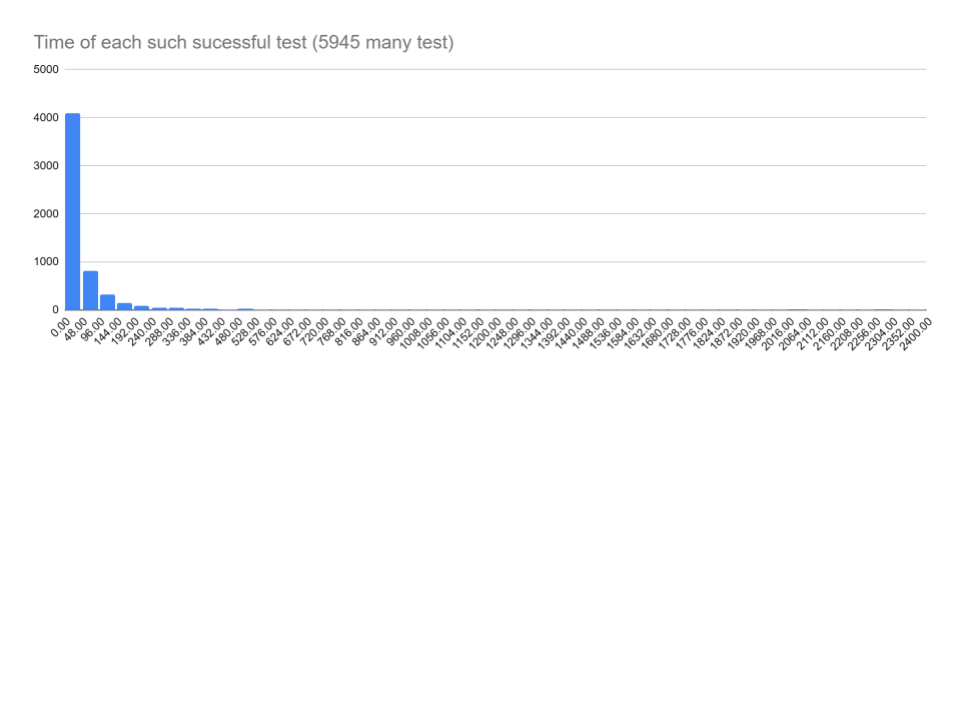
We conducted an experiment on 10,000 cases, randomly selecting coefficients for degree 3 rational functions. For each case, we randomly chose a value for alpha and set the limit level to 9, before performing a test. We continued the test until we either achieved success or reached 10 attempts, after which we deemed the result indeterminable

Datas: Time(ms)

Datas: Level

level-number

Discussion

  1. Out of 10,000 cases tested, 82 (1.38%) failed the check but did not demonstrate any composition relation
  2. The algorithm is forced to be efficient. It is hard to determine the lower bound of $$|h_f(\alpha)-h_g(\alpha)|$$ when the difference is not zero.

Thank you