- Compute the following double integral
- $\int\int_{\Omega}\frac{1}{1+x+y}dxdy$, $\Omega: [0,1]\times[0,2]$. (Hint: it requires integration by part for $\int\ln(x)dx$.)
- $\int\int_{\Omega}\frac{xy}{(x^2+y^2)^2}dxdy$, $\Omega:[1,2]\times[1,3]$. (Hint: we are going to apply integration by part twice.)
- Explain $\int\int_{\Omega}1dxdy$ is the area of $\Omega$.
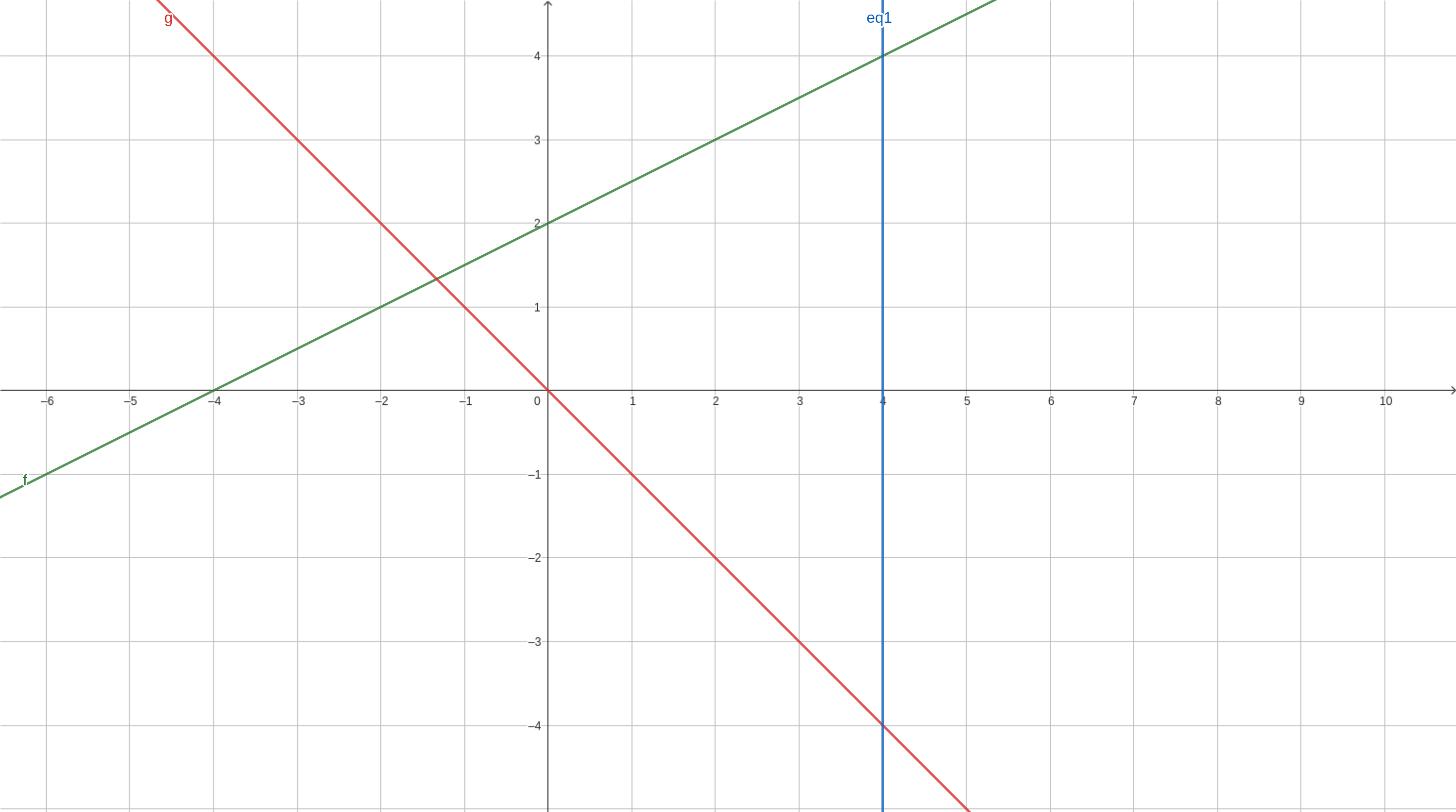
- Examine the region $\Omega$ bounded by the lines $x=4$, $y=\frac{1}{2}x+2$, and $y=-x$, as depicted in the figure below. Find the limits of $x$ and $y$ for $\Omega$.
- Consider the region $\Omega$ defined by $0 < x < 2$ and $0 < y < x^2$. Rewrite the inequality so that instead of bounding $x$ by constants and bounding $y$ by functions, we will bound $y$ by constants and $x$ by functions.
ChatGPT Answer checking(beta)
- API Key: You can get your key by following the following steps link
-
- Your answer of 1-1:
[correct/incorrect]
- Your answer of 1-2:
[correct/incorrect]
- Your answer of 1-1:
- Your answer of 2:
[correct/incorrect]
- Your answer of 3:
[correct/incorrect]
-
Your answer of 4:
[correct/incorrect]