Calculus 2 Homework 2 Answers

Method 1 (Cylindrical Sehlls Method) The integral \(\int_{R-r}^{R+r}2\pi\cdot x\cdot 2\sqrt{r^2-(x-R)^2}dx\) is the volume. We apply the trig sub by letting $x-R = r\sin\theta$ and $dx = r\cos\theta d\theta$ with $\theta\in[-\pi/2, \pi/2]$ to calculate this integral. That is \(\int 2\pi\cdot x\cdot 2\sqrt{r^2-(x-R)^2}dx = \int 4\pi (R+r\sin\theta)\cdot r\cos\theta\cdot r\cos\theta d\theta = \int 4\pi r^2R\cos^2\theta + 4\pi r^3\sin\theta\cos^2\theta d\theta.\) Note that the second integral is an odd function and $\theta$ is from $-\pi/2$ to $\pi/2$, so this integral is $0$. We use double angle formula to simplify the first part. It follows \(\int 4\pi r^2R \cos^2\theta d\theta = \int 4\pi r^2R \frac{\cos(2\theta)+1}{2} d\theta = \int 2\pi r^2R\cos(2\theta)d\theta + \int 2\pi r^2R d\theta\). We can again ignore the first integral because $2\theta$ will be range from $-\pi$ to $\pi$ and the definite integral of cosine function on a period is $0$. The second integral is $2\pi^2 r^2R$.

Method 2 (Washer Method) The integral \(\int_{-r}^r \pi [(\sqrt{r^2-y^2}+R)^2 - (-\sqrt{r^2-y^2}+R)^2] dy\) is the volume. We simplify the integral \(\int_{-r}^r \pi [(\sqrt{r^2-y^2}+R)^2 - (-\sqrt{r^2-y^2}+R)^2] dy = \int_{-r}^r \pi 4R\sqrt{r^2-y^2}d\theta.\) Let $y=r\sin\theta$, $dy = r\cos\theta d\theta$, and the range of $\theta$ is from $-\pi/2$ to $\pi/2$. It follows \(\int_{-r}^r \pi 4R\sqrt{r^2-y^2}d\theta = \int_{-\pi/2}^{\pi/2} 4\pi r^2R \cos^2\theta d\theta = 2\pi^2r^2R.\)

The following figure demonstrate how we are going to partition the area. 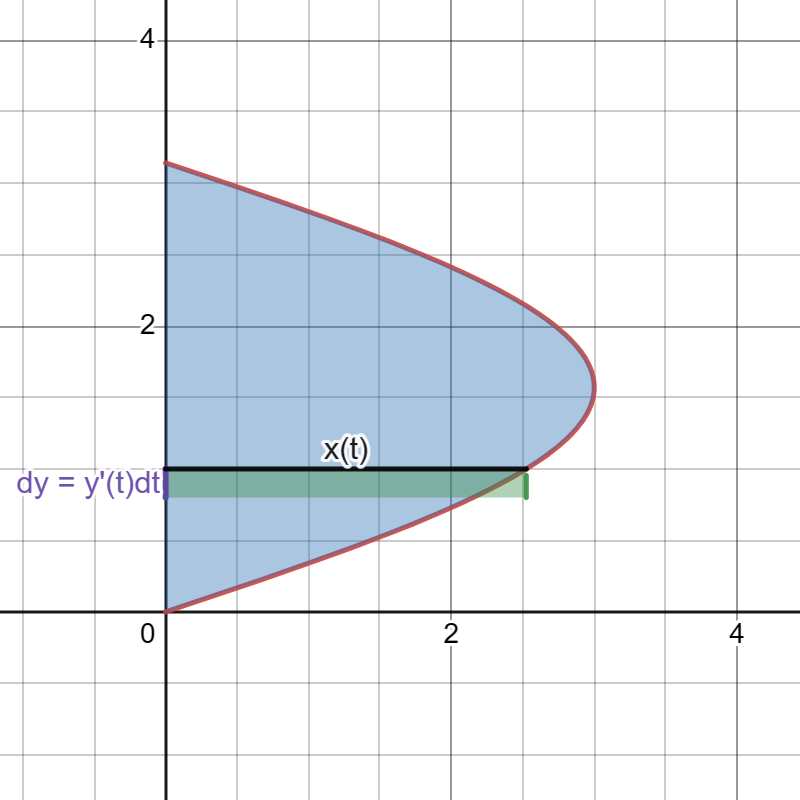The tiny area is $x(t)y’(t)dt$, so the area of the region enclosed by the curves is $\left|\int_{a}^b x(t)y’(t)dt\right|$

We can partition the surface into bands (see figure). To estimate the area of a band, we can pretend it is a rectangle when we unfold the band on table. The width of the band can be denote by $\sqrt{dx^2+dy^2}$, and the length can is $2\pi f(x)$. Thus, we derive that the area of the surface is \(\int_a^b 2\pi f(x)\sqrt{dx^2+dy^2} = \int_a^b 2\pi f(x)\sqrt{1+f'(x)^2}dx.\)

1. Apply the implicit differentiation to the equation, we get $\frac{2}{3}x^{-1/3} + \frac{2}{3}y^{1/3}y’ = 0$. Thus, $y’ = -\left(\frac{y}{x}\right)^{1/3}$. Using the formula of arc length, we have \(L = \int_{0}^1 \sqrt{1+\frac{y}{x}^{2/3}}dx = \int_0^1 x^{-1/3}dx = \frac{3}{2}.\)
2. Using the formula that we found in the previous question, the area of the surface is $\int_{0}^12\pi(1-x^{2/3})^{3/2}\sqrt{1+\frac{y}{x}}dx.$ We calculate this integral \(\begin{align} \int 2\pi(1-x^{2/3})^{3/2}\sqrt{1+\left(\frac{y}{x}\right)^{2/3}}dx &= \int 2\pi(1-x^{2/3})^{3/2}x^{-1/3}\sqrt{x^{2/3}+y^{2/3}}dx\\\\ &= \int 2\pi(1-u^2)^{3/2} u^{-1} 3 u^2 du\ (u=x^{1/3},\text{ so }du = \frac{1}{3}x^{-2/3}dx = \frac{1}{3}u^{-2}dx)\\\\ &= \int -3\pi w^{3/2} dw\ (w = 1-u^2,\text{ so }dw = -2udu)\\\\ &= \frac{6\pi}{5}w^{5/2} = \frac{6\pi}{5}(1-u^2)^{5/2} = \frac{6}{5}(1-x^{2/3})^{5/2}. \end{align}\) Thus, $\int_{0}^12\pi(1-x^{2/3})^{3/2}\sqrt{1+\frac{y}{x}}dx = \left. \frac{6\pi}{5}(1-x^{2/3})^{5/2}\right|_0^1 = \frac{6\pi}{5}$.