Counterexamples for Fubini’s theorem
Example 1
The idea of constructing a counterexample for Fubini’s theorem comes from the following infinite matrix:
\[\begin{bmatrix} 1 & 0 & 0 & 0 & \cdots\\\\ -1 & 1 & 0 & 0 & \cdots\\\\ 0 & -1 & 1 & 0 & \cdots\\\\ 0 & 0 & -1 & 1 & \cdots\\\\ \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}\]We place $1$ on the diagonal and $-1$ beneath the diagonal. Thus, the double sum $\sum_i\sum_ja_{ij}$ is not equal to the double sum $\sum_j\sum_ia_{ij}$. Hence, the order of summation matters. This matrix inspires the following definition:
\[f(x,y)=\begin{cases} \frac{1}{2^{2n}}, & 2^{n-1}\leq x^{-1}, y^{-1}< 2^n\\\\ \frac{-1}{2^{2n+1}}, & 2^{n-2}\leq x^{-1}\leq 2^{n-1}\leq y^{-1}\leq 2^{n}\\\\ 0, & (x,y)\not\in[0,1]^2 \end{cases}\]Then, the order of iterated integral of $f$ matters. The following figure illustrates how we assign the value of $f$.
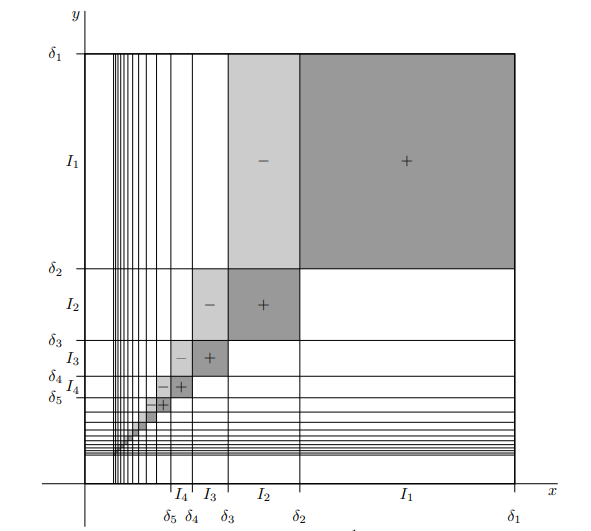
Example 2
Certain functions, even when written as a combination or composition of basic functions, can still violate Fubini’s theorem. For example, let us consider $f(x,y)=\frac{x^2-y^2}{(x^2+y^2)^2}$. We have
\[\int_0^1\int_0^1\frac{x^2-y^2}{x^2+y^2}dxdy = -\int_0^1\int_0^1\frac{x^2-y^2}{x^2+y^2}dydx\]Type I & II regions
Type I regions are regions that are bounded by vertical lines $x=a$ and $x=b$, and curves
$y=g(x)$ and $y=h(x)$, where we assume that $g(x)<h(x)$ and $a<b$. Then we can integrate first over
\[\int_a^b\int_{g(x)}^{h(x)} f(x,y)dydx\]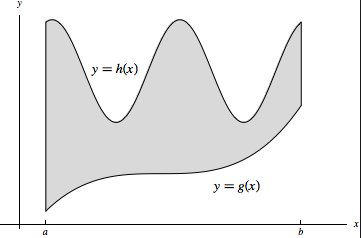
Type II regions are regions that are bounded by vertical lines $y=c$ and $y=d$, and curves
$x=g(y)$ and $x=h(y)$, where we assume that $g(x)<h(x)$ and $c<d$. Then we can integrate first over
\[\int_c^d\int_{g(x)}^{h(x)}f(x,y)dxdy\]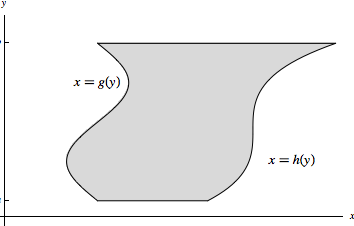
Which one to use?
Sometimes the choice between one type and another is clear. If you draw any vertical line from boundary to boundary, and the line is within the region, then it must be Type I. Similarly, if any horizontal line drawn from boundary to boundary is within the region, then it must be Type II. However, if the region is convex, like a circle, then any line must be within the region. In this situation, you would write your region as either Type I or Type II, depending on which is easier to integrate or has a more straightforward form of inequalities.
An advanced question must involve the process of changing expressions in the region. For example, the integral
\[\int_0^8\int_{x^{1/3}}^2\frac{1}{1+y^4}dydx\]may appear difficult to integrate at first glance. However, after changing the expression to Type II, the integral becomes
\[\int_0^2\int_0^{y^3}\frac{1}{1+y^4}dxdy\]should be easier to handle.
citations:
- The graphs for type I and II regions are directly sourced from https://web.ma.utexas.edu/users/m408s/m408d/CurrentWeb/LM15-3-2.php
- The graph used to illustrate the counterexample of Fubini’s theorem is sourced from https://personal.math.ubc.ca/~feldman/m226/fubini.pdf