Definition of Triple Integrals
In the simplest terms, a triple integral can be thought of as an integral of a function over a three-dimensional region. Just like a double integral can be used to find the area of a plane region, a triple integral can be used to find the volume of a space region.
In terms of Riemann sum, a function $h(x,y,z)$ over a box $B=[a,b]\times[c,d]\times[e,f]$ is integrable if the limit
\[\iiint_Bh(x,y,z)dV = \lim_{l,m,n\to\infty}\sum_{i=1}^l\sum_{j=1}^m\sum_{k=1}^n h(x_i^\ast,y_j^\ast,z_k^\ast)\Delta V\]exists. At first glance, the limit may appear abstract, but it actually generalizes the Riemann sum for one dimension. To extend the triple integral to any region $R$ with a “nice” boundary, we consider a sufficiently large box $B$ containing $R$. We then define a new function that extends the original one as follows:
\[F(x,y,z)=\begin{cases} h(x,y,z),\quad (x,y,z)\in R\\\\ 0,\quad (x,y,z)\in B\setminus R \end{cases}\]Fubini’s Theorem
Fubini’s theorem asserts that a triple integral can be computed using an iterated integral if the function being integrated is continuous over the box $B$. Specifically, we have:
\[\iiint_Bh(x,y,z)dV=\int_a^b\int_c^d\int_e^fh(x,y,z)dzdydx\]Let us now move on to more general 3 dimensional regions.
Type I, II, and III Regions
We have three distinct general region. Let us scketch them one by one.
Type I regions Let $D$ represent the projection of $R$ onto the $xy$-plane, and, for any fix $(x,y)$, $z$ is bounded above and below by $u_2(x,y)$ and $u_1(x,y)$ respectively. Then, we can express $R$ as
\[\\{(x,y,z)|(x,y)\in D,\quad u_1(x,y)\leq z\leq u_2(x,y)\\}\]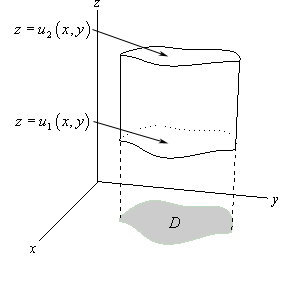
Type II regions Let $D$ represent the projection of $R$ onto the $yz$-plane, and, for any fix $(y,z)$, $x$ is bounded above and below by $u_2(x,y)$ and $u_1(x,y)$ respectively. Then, we can express $R$ as
\[\\{(x,y,z)|(y,z)\in D,\quad u_1(y,z)\leq x\leq u_2(y,z)\\}\]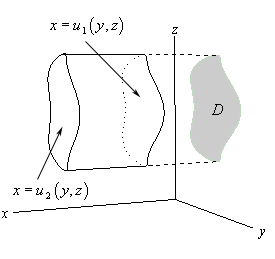
Type I regions Let $D$ represent the projection of $R$ onto the $xz$-plane, and, for any fix $(x,z)$, $y$ is bounded above and below by $u_2(x,y)$ and $u_1(x,y)$ respectively. Then, we can express $R$ as
\[\\{(x,y,z)|(x,z)\in D,\quad u_1(x,z)\leq y\leq u_2(x,y)\\}\]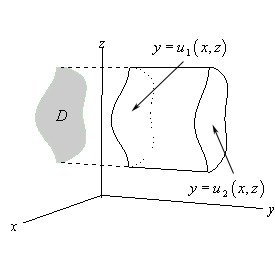
Region D
The region $D$ can be further expressed as a type I or II plane region. Therefore, there are $3\times 2$ total possibilities. Let’s use an example to demonstrate how to form an integral using this concept.
Suppose $R$ is type I and $D$ is type I. Then, $R$ can be expressed as
\[\\{(x,y,z)|a\leq x\leq b, c(x)\leq y, d(x), u_1(x,y)\leq z\leq u_2(x,y)\\},\]and the correspondent iterated integral is
\[\iiint_Rf(x,y,z)dV = \int_a^b\int_{c(x)}^{d(x)}\int_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dzdydx.\]Which one to use?
Similar to a planar region, we draw lines parallel to the $x$, $y$, and $z$ axes. If every line parallel to the $z$-axis intersects the region from one boundary to the other, then $R$ is a type I region. To determine whether a region is type II or III, we use the same logic with lines parallel to the $x$-axis and $y$-axis, respectively.
Applications
Volume
The volume of a solid $E$ is
\[\iiint_EdV.\]Mass
If a solid $E$ has a density $\rho(x,y,z)$ at each point $(x,y,z)$ in $E$, then the mass of $E$ is
\[m=\iiint_Ef(x,y,z)dV\]Moment
If a solid $E$ has a density $\rho(x,y,z)$ at each point in $E$, then the moments are
\[M_{yz}=\iiint_E x\rho(x,y,z) dV,\quad M_{xz}=\iiint_E y\rho(x,y,z)dV, \quad\text{and }M_{xy}=\iiint_E z\rho(x,y,z)dV\]Center of mass
The center of mass is
\[(\bar{x},\bar{y},\bar{z})=\left(\frac{M_{yz}}{m},\frac{M_{xz}}{m}, \frac{M_{xy}}{m}\right).\]If the density is constant, the center of mass of the solid is called the centroid of $E$.
Moment of inertia
The moments of inertia about the three coordinate axes for a solid $E$ that has a density $\rho(x,y,z)$ at each point in $E$ are
\[I_x = \iiint_E(y^2+z^2)\rho(x,y,z)dV,\] \[I_y = \iiint_E(x^2+z^2)\rho(x,y,z)dV,\]and
\[I_z = \iiint_E(x^2+y^2)\rho(x,y,z)dV\]Cylindrical Coordinate
Cylindrical Coordinate System is an extension of the two-dimensional polar coordinate system to three dimensions. It is a way to generalize the polar coordinate system by extending it into the third dimension via a z-coordinate. This system becomes particularly useful when dealing with problems that involve cylindrical symmetry, where objects and properties are invariant under rotations around one axis.
A point $(x,y,z)$ in a three dimensional space can be expressed as $(r,\theta,z)$ where
\[r=\sqrt{x^2+y^2},\quad \theta=\arctan\left(\frac{y}{x}\right).\]To change coordinates from Euclidean to cylindrical, we proceed as follows:
\[x=r\cos(\theta),\quad y=r\sin(\theta),\quad\text{and }z=z.\]Integration on Cylindrical Coordinate
We have
\[\iiint_Ef(x,y,z)dxdydz=\iiint_Ef(r\cos\theta,r\sin\theta,z)\left|\frac{\partial(x,y,z)}{\partial(r,\theta,z)}\right|drd\theta dz\]where the Jacobian is
\[\left|\frac{\partial(x,y,z)}{\partial(r,\theta,z)}\right|=\det\left(\begin{matrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z}\\\\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z}\\\\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z} \end{matrix}\right)=r\]Citations:
- The picture on this page was copied from Calculus III - Triple Integrals (lamar.edu)