| We’re considering a change of variables where $x=u^2-v^2$ and $y=2uv$. We aim to express the solid $E=\{(x,y) | 0\leq y\leq 2,\frac{y^2+4}{4}\leq x\leq -\frac{y^2+4}{4}\}$ in terms of $u$ and $v$. Let’s examine the following graph to better understand what we’re trying to achieve. We are seeking the area on the left-hand side marked by ??? which will transform into the area enclosed by the blue curves on the right-hand side. |
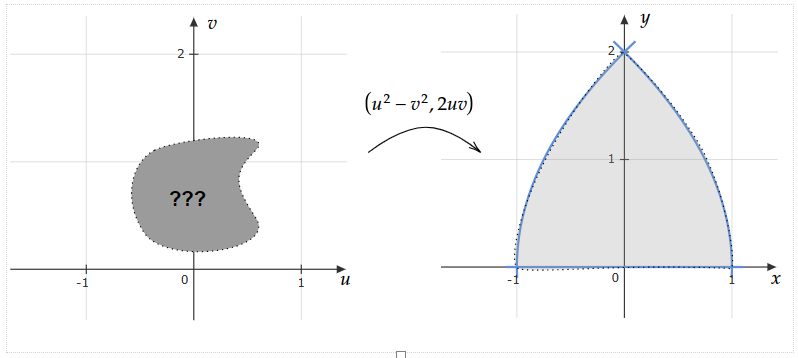
If we can find the inverse function of $(u^2-v^2,2uv)$, and express $u$ and $v$ in terms of $x$ and $y$, we can directly map the area on the right to the area of interest.
We will solve for $u$ and $v$ using the equations $x=u^2-v^2$ and $y=2uv$. We observe $x^2+y^2=(u^2+v^2)^2$. From this, we can deduce that $u^2=\frac{\sqrt{x^2+y^2}+x}{2}$ and $v^2 = \frac{\sqrt{x^2+y^2}-x}{2}$.
Then, the boundary (blue curves) must map to the boundary of ??? (why). Therefore, we only need to examine the results of $y=0$, $y^2=x+4$, and $y^2=-x+4$.
-
$\bm{y=0}$: we have $u^2=\frac{ x +x}{2}$ and $v=\frac{ x -x}{2}$. If $x>0$, then we have $u^2=x$ and $v=0$. If $x<0$, we have $u^2=0$ and $v^2=-x= x $. -
$\bm{y^2=4x+4}$: we have $u^2=\frac{ x+2 +x}{2}$ and $v^2=\frac{ x+2 -x}{2}$, and note that $-1\leq x\leq 0$ implies that $u^2=x+1$ and $v^2=1$. -
$\bm{y^2=-4x+4}$: we have $u^2=\frac{ x-2 +x}{2}$ and $v^2=\frac{ x-2 -x}{2}$, and note that $0\leq x\leq 1$ implies that $u^2=1$ and $v^2=1-x$
The three items mentioned above can be simplified and represented in the following graph.
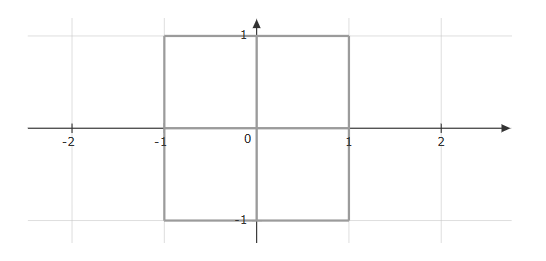
The “田” shapes are possible lines that maps to the blue curves in the first picture via the map $(u^2-v^2,2uv)$. Moreover, we know that $2uv>0$, so the only possibilities are the green square and purple square in the following figure.
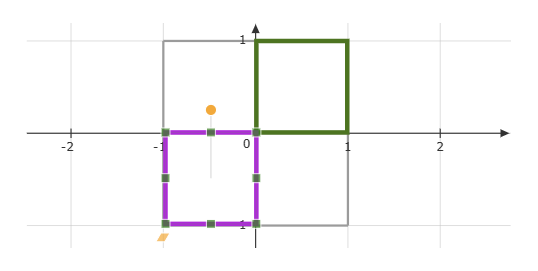
Regarding the integration of $\iint_RydA$ by changing the variables, which square should we use? The answer is “it doesn’t matter.” You can check this yourself.