Spherical coordinates, also known as spherical polar coordinates, are a system of coordinates used in three-dimensional space. They are especially useful in fields such as physics and engineering where problems often involve three dimensions. In spherical coordinates, a point in space is represented by three values: the radial distance from the origin, the polar angle, and the azimuthal angle.
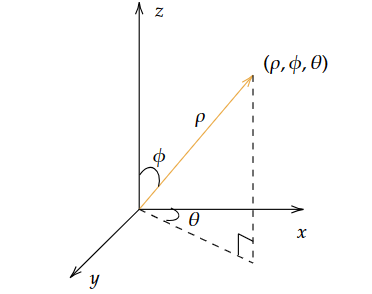
A point $(x,y,z)$ in Euclidean coordinate can be obtained from its spherical coordinate $(\rho, \phi, \theta)$, where $r\in[0,\infty]$, $\phi\in[0,\pi]$, and $\theta\in[0,2\pi]$, by
\[x=\rho\sin(\phi)\cos(\theta),\text{ }y=\rho\sin(\phi)\sin(\theta),\text{ and }z=\rho\cos(\phi)\]From the last eqaulity, we obtain $\phi=\arccos(\frac{z}{\rho})$. This could be useful in determining the limits of $\phi$ in a triple integral.

Integration on a spherical coordinate
Given a solid $E$ that can be expressed in spherical coordinate, we can integrate $f(x,y,z)$ over $E$ by the triple integral
\[\iiint_Ef(\rho\sin(\phi)\cos(\theta),\rho\sin(\phi)\sin(\theta),\rho\cos(\phi))\rho^2\sin(\phi)d\rho d\phi d\theta.\]The $\rho^2\sin(\phi)$ is obtained by the jacobian
\[\left|\frac{\partial(x,y,z)}{\partial(\rho,\phi,\theta)}\right| = \det\left( \begin{matrix} \sin(\phi)\cos(\theta) & \rho\cos(\phi)\cos(\theta) & -\rho\sin(\phi)\sin(\theta)\\\\ \sin(\phi)\sin(\theta) & \rho\cos(\phi)\sin(\theta) & \rho\sin(\phi)\cos(\theta)\\\\ \cos(\phi) & -\rho\sin(\phi) & 0 \end{matrix}\right).\]Geometric point of view
The following graph illustrates our estimation of a small cube partition using spherical coordinates.
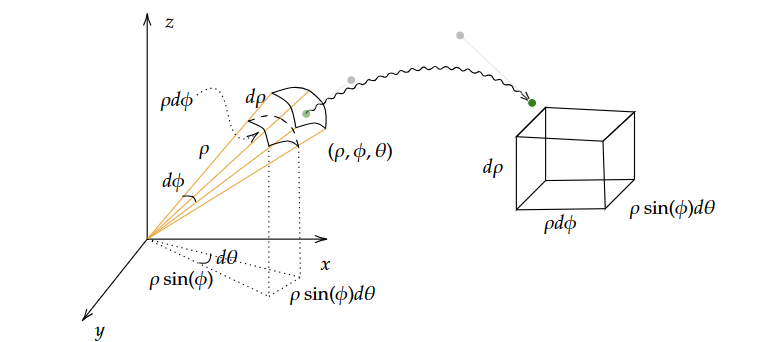
We can interpret $\rho^2\sin(\phi)$ as the ratio of volume change when we switch the measure from $dxdydz$ to $d\rho d\phi d\theta$.