Green’s Theorem is a fundamental concept in vector calculus that establishes a relationship between a line integral around a simple closed curve and a double integral over the plane region it encloses. Named after the British mathematician George Green, this theorem serves as a vital tool in physics and engineering for solving problems related to fluid flow, electricity, and magnetism.
Theorem(Green). Let $F(x,y)=P(x,y)i+Q(x,y)j$ be a vector field in $C^1$ class. For a positively oriented, piecewise smooth simple closed curve C and the region D it encloses, i.e. $\partial D=C$, we have
\[\int_CPdx+Qdy=\iint_D\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dA\]Green’s Theorem can be intuitively understood by thinking of the left side of the equation as the circulation around the boundary of a region, and the right side as the sum of the circulations around infinitesimally small loops within the region. In other words, the total circulation around the boundary of a region is equal to the sum of the circulations within the region. This theorem essentially bridges the gap between local behavior (differential forms) and global behavior (integral forms) in a two-dimensional field. We will show more details when we introduce curl.
proof. We will only prove Green’s theorem when $D$ is a type one and also a type two region.
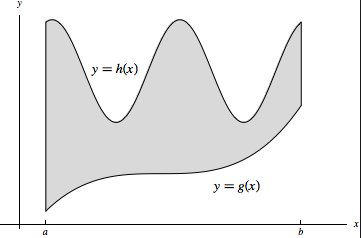
We claim
\[\int_CPdx = -\iint_D\frac{\partial P}{\partial y}dydx\quad\text{and}\quad\int_CQdy =\iint_D\frac{\partial Q}{\partial x}dydx.\]| Use the assumption that $D$ is of type one, we can show the left equality. Let $D=\{(x,y) | a\leq x\leq b, g(x)\leq y\leq h(x)\}$. Then, a direct computation confirms the equality, that is |
Note that these two integrals represent the line integral with respect to $x$ on the top and bottom curves that bound $D$. Moreover, the vertical line has $dx=0$, so $\int_{x=a}Pdx=\int_{x=b}Pdx = 0$. Therefore, we have
\[\begin{align*} \int_a^bP(x,h(x))dx&+\int_b^aP(x,g(x))dx = \int_a^bP(x,h(x))dx+\int_b^aP(x,g(x))dx\\\\ &=\int_a^bP(x,h(x))dx+\int_b^aP(x,g(x))dx + \int_{x=a}Pdx+\int_{x=b}Pdx\\\\ &=\int_CPdx. \end{align*}\]Similarly, using the assumption that $D$ can be expressed as a type two region, we can show the other equality.
Finding Area by Green’s Theorem
We know that $A(D)=\iint_DdA$. So, to use Green’s theorem to find area, we require to find $P$ and $Q$ such that
\[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=1\]The solution of $P$ and $Q$ are not unique, and we have the following three candidates:
\[\begin{cases} P=0\\\\ Q=x \end{cases},\quad \begin{cases} P=-y\\\\ Q=0 \end{cases},\quad\text{and}\quad \begin{cases} P=-\frac{1}{2}y\\\\ Q=\frac{1}{2}x \end{cases}\]Extended Versions of Green’s theorem
To extend the application of Green’s theorem to more general regions, consider the example of a donut-shaped region, also known as an annular region $D$ (bounded by outer and inner circles). This region is not simple as it contains a hole. To apply Green’s theorem, divide the annular region into upper and lower half. For the upper half of the semiannular, we provide a positively oriented path represented by $C_1+C_2+C_3+C_4$. Similarly, for the lower half of the semiannular, the positively oriented path is represented by $C_1’+C_4’+C_3’+C_2’$.

Since $C_2$ and $C_2’$ (as well as $C_4$ and $C_4’$) are in opposite directions, their line integrals will cancel out. That is
\[\begin{align*} &\int_{C_1}Fd\gamma + \int_{C_2}Fd\gamma + \int_{C_3}Fd\gamma + \int_{C_4}Fd\gamma + \int_{C'_1}Fd\gamma + \int_{C'_2}Fd\gamma + \int_{C'_3}Fd\gamma + \int_{C'_4}Fd\gamma\\\\ &=\int_{C_1+C_1'}Fd\gamma - \int_{-(C_3+C_3')}Fd\gamma \end{align*}\]Let $B$ (big circle) be the region bounded by outer circle, and let $B’$e (small circle) be the region bounded by the inner circle. Applying Green’s theorem to $C_1+C_1’$ and $-(C_3+C_3’)$, we have
\[\begin{align*} \int_{C_1+C_1'}Fd\gamma - \int_{-(C_3+C_3')}Fd\gamma &= \iint_B\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dA - \iint_{B'}\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dA\\\\ &= \iint_D\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dA. \end{align*}\]The extended version of Green’s theorem is frequently used to demonstrate that the integral of a loop does not depend on the loop’s path or initial point, but solely on the number of poles (undefined point) provided by the function.
Proof of the Criteria for a Conservative Vector Field
Recall the theorem of the criteria for a conservative vector field.
Theorem. Suppose $D$ is an open, connected domain, and $F$ is a vector field on $D$ that is of class $C^1$. If $\int_C F\cdot d\gamma$ is path independent for every path $C$ in $D$, then $F$ is a conservative vector field, that is, $F=\nabla f$ for some potential function $f$ on $D$.
We need to demonstrate that for every closed curve $C$, we have $\int_CF\cdot d\gamma=0$. This claim is straightforward for a simple closed curve $C$ due to Green’s theorem. To generalize this argument for non-simple closed curves, consider a curve $C$ in the shape of an 8, for example. It can be broken down into two simple closed curves, which allows us to extend the result to any closed curve.