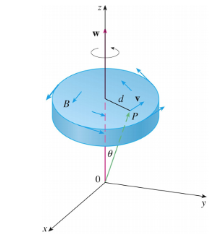
- This exercise demonstrates a connection between the curl vector and rotations. Let $B$ be a rigid body rotating about the $z$-axis. The rotation can be described by the vector $\mathbf{w}=\omega\mathbf{k}$, where $\omega$ is the angular speed of $B$, that is, the tangential speed of any point $P$ in $B$ divided by the distance $d$ from the axis of rotation. Let $\mathbf{r}=\langle x,y,z\rangle$ be the position vector of $P$.
- By considering the angle $\theta$ in the figure, show that the velocity field of $B$ is given by $\mathbf{v}=\mathbf{w}\times\mathbf{r}$.
- Show that $\mathbf{v}=-\omega y\mathbf{i}+\omega x\mathbf{j}$.
-
Show that curl $\mathbf{v}=2\mathbf{w}$.
- Let $z$ be a complex number $x+yi$ where $i$ is the imaginary number, i.e., $i^2=-1$. In the following questions, we will step-by-step demonstrate that $\int_C\frac{1}{z}dz=2\pi i$ for any simply closed curve that encloses the origin.
- Rewrite the complex function $f(z)=\frac{1}{z}$ as a vector field $F(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}$ in $\mathbb{R}^2$.
- Suppose $dz=dx+idy$. Find vector fields $G_1$ and $G_2$ such that $\frac{1}{z}dz=G_1\cdot d \gamma + iG_2\cdot d\gamma$.
- Show that, for $l=1$ and $2$, $\int_{C_1}G_ld\gamma=\int_{C_2}G_ld\gamma$ for any two simply closed paths that enclose the origin.
- Show that $\int_{C}G_1\cdot d\gamma =0$ and $\int_CG_2\cdot d\gamma=2\pi$ for any closed simple curve $C$ enclosing the origin.