Divergence and its connection with Green’s theorem
Let us recall $d\gamma = dx\mathbf{i}+dy\mathbf{j}$, and $ds=\sqrt{dx^2+dy^2}$. Thus, we have
\[d\gamma = \left(\frac{dx}{\sqrt{dx^2+dy^2}}\mathbf{i}+\frac{dy}{\sqrt{dx^2+dy^2}}\mathbf{j}\right)\sqrt{dx^2+dy^2} = Tds\]where $T$ is the unit vector parallel to $dx\mathbf{i}+dy\mathbf{j}$. So, we can also rewrite Green’s theorem in the following form
\[\int_{\partial D} F\cdot Tds = \iint_D Q_x-P_ydA.\]If we replace the vector $T$ with its unit normal vector that points outward from region $D$, we get a different form of Green’s theorem. Note that there are two unit vectors normal to $T$, given by $\frac{\pm 1}{\sqrt{dx^2+dy^2}}(dy\mathbf{i} - dx\mathbf{j})$. The normal vector pointing outward from region $D$ always points to the right when we face in the direction of $T$. Using the cross product, we know that we should choose the positive sign for the right vector $N$. Therefore, we can conclude
\[\int_{\partial D}F\cdot Nds = \int_{\partial D}Pdy-Qdx =\int_{\partial D}F^t\cdot d\gamma\]where $F^t = -Q\mathbf{i}+P\mathbf{j}$ is the vector field perpendicular to $F$. Thus, by Green’s theorem, we have
\[\int_{\partial D}F\cdot Nds=\iint_{D}Q_y+P_xdA.\]We refer to these two different versions of Green’s theorem as the Circulation form and the Flux form for distinction. We also note that
\[\iint_DP_x+Q_ydA =\iint_D\text{div}(F)dA\]Parametric Surface
A parametric surface (or vector function) is a function $r:\mathbb{R}^2\to\mathbb{R}^3$, represented as
\[r(u,v)=x(u,v)\mathbf{i}+y(u,v)\mathbf{j}+z(u,v)\mathbf{k}\]where $x$, $y$, and $z$ are real-valued functions.
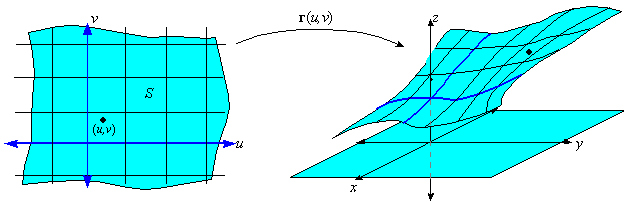
The rigid grid on the $uv$-coordinate naturally generates a grid on the parametric surface. The following examples represent typical parametric surfaces that we will continue to revisit for study.
Example. (Cylinder) A cylinder can be naturally parametrized as follows:
\[r(\theta,z)=\cos(\theta)\mathbf{i}+\sin(\theta)\mathbf{j}+z\mathbf{k}\]| for $(\theta,z)\in\{(\theta,z) | 0\leq\theta\leq 2\pi, z\in\mathbb{R}\}.$ |
Example. (Sphere) A sphere of radius $a$ can be parametrized by spherical coordinate as follows:
\[r(\phi,\psi)=a\sin\phi\cos\psi\mathbf{i}+a\sin\phi\sin\psi\mathbf{j}+a\cos\phi\mathbf{k}\]for $0\leq \phi<\pi$ and $0\leq \psi<2\pi$.
Example. (Graph) The vector function representing a graph $z=f(x,y)$ is as follows:
\[r(x,y)=x\mathbf{i}+y\mathbf{j}+f(x,y)\mathbf{k}.\]Example. (Surface of revolution) The surface obtained by rotating the graph $y=f(x)$ for $0\leq x\leq b$ around $x$-axis can be parametrized as:
\[r(x,\theta)=x\mathbf{i}+f(x)\cos\theta\mathbf{j}+f(x)\sin\theta\mathbf{k}\]for $a\leq x\leq b$ and $0\leq \theta\leq 2\pi$.
Examples. Parametric surfaces can exhibit intricate structures. For instance, they might form a surface that overlaps itself, or an unorientable surface like a Möbius strip.
Tangent Plane
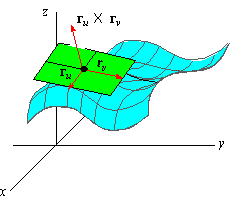
Let $P$ be a point in the domain of $r$. Suppose the first partial derivatives of $r$ are continuous near $P$. Then, $r_u(P)$ and $r_v(P)$ will be two vectors. These vectors can be used to span the entire tangent plane. In other word, $r_u\times r_v$ is a normal vector of the tangent plane at $P$.
- Parametric surface’s figure is from https://math.etsu.edu/multicalc/prealpha/Chap3/Chap3-4/part2.htm
- The figure use for tangent plane is from https://math.etsu.edu/multicalc/prealpha/chap3/chap3-6/part2.htm
