Area of Parametric Surface
We can use the Riemann sum to approximate the surface area $A(S)$, and define the surface area as the limit of this Riemann sum. To write down Riemann sum, we first give a partition (by grid) on $D\subseteq \mathbb{R}^2$, the domain of a parametric surface $r:D\subseteq \mathbb{R}^2\to\mathbb{R}^3$.
| A patch, a rectangular region $\Delta u\Delta v$ on $\mathbb{R}^2$ a rectangle on $D$ denote as $R_{ij}$, is mapped to a parallelogram on $S$, denoted as $S_{ij}$, by the parametric surface $r$. Then the surface area of $S_{ij}$ is approximated by $ | r_u \times r_v | dudv$. |
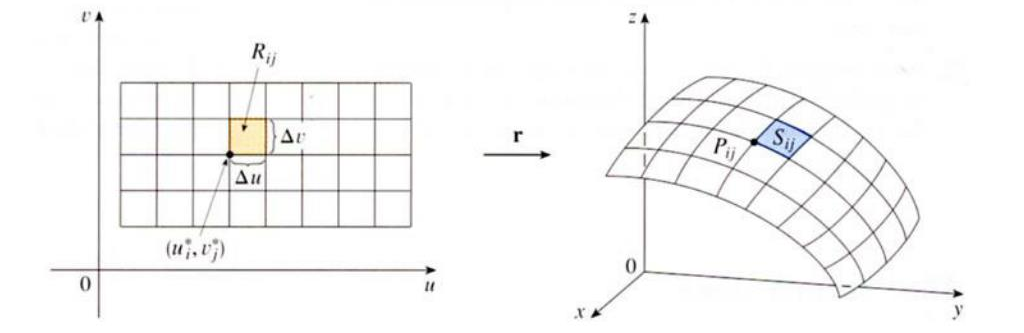
| Thus, the surface area $A(S)$ can be approximate by its Riemann sum $\displaystyle\sum_{i=1}^{m}\sum_{j=1}^nA(S_{ij})\approx\sum_{i=1}^{m}\sum_{j=1}^n | r_u\times r_v | \Delta u\Delta v$. his leads to the following definition. |
| Definition. The area of a parametric surface $S$, denoted by $A(S)$, is defined as the double integral $\displaystyle A(S)=\iint_D | r_u\times r_v | dudv$. This is also known as the surface integral of $S$ over $D$. |
Remark. If you’re wondering why we use a definition here, it’s because there’s no direct way to compute the surface area. All computations are approximations, so a formula for surface area can only be assessed based on its sensibility. A sensible formula means that the estimated result matches the value computed from other methods and aligns with the area that we can directly compute.
Surface Integral
Let $f:K\subseteq\mathbb{R}^3\to \mathbb{R}$ represent a real-valued function defined on $K$. Let $S$ denote a surface with a parametric surface $r:D\to S$, and $K$ contains $S$. We define the double integral over $S$, $\iint_SfdS$, as the limit of the Riemann sum
\[\sum_{i=1}^m\sum_{j=1}^nf(x_i^\ast,y_i^\ast,z_i^\ast)A(S_{ij})\]| Using the relation $A(S_{ij})\approx | r_u\times r_v | \Delta u\Delta v$, the following formula can be derived: |