Two lines in general positions typically intersect at a point. Only in specific cases—when lines are parallel or overlapping—does this intersection not occur. This concept explains why we call a system of $n$ equations in $n$ unknowns nonsingular when it has a unique solution, and singular otherwise.
We aim to explore three deeper aspects of linear equation systems:
- The geometry of planes
- Matrix notation and Gaussian elimination
- Matrix decomposition using elementary matrices
The Geometry of Linear equations
There are two approaches to reading a linear equation system: horizontal and vertical. We can examine the system by rows or by columns. Let’s explore both perspectives.
The nonsingular case
First, let’s focus on individual equations (rows).
Example. Let’s consider
\[\begin{align*} 2x-y=1\\\\ x+y=5 \end{align*}\]By row (horizontal), this system of course represents two straight line in the $xy$-plane (see Figure 1).
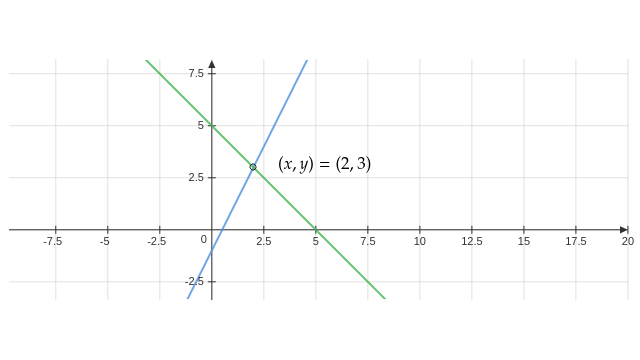
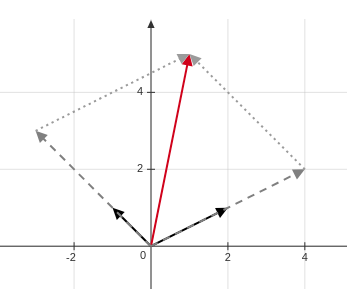
By column (vertical), the two separate equations are really one vector equation:
\[\textbf{Column form}\qquad x\begin{bmatrix}2\\\\1\end{bmatrix}+y\begin{bmatrix}-1\\\\1\end{bmatrix}=\begin{bmatrix}1\\\\5\end{bmatrix}.\]The goal is to find a combination of the column vectors on the left side that yields the vector on the right side. Geometrically, we’re seeking the proper scales for the two vectors $\begin{bmatrix}2\\1\end{bmatrix}$ and $\begin{bmatrix}-1\\1\end{bmatrix}$ so that $\begin{bmatrix}1\\5\end{bmatrix}$ is at the vertex opposite the origin in the parallelogram formed by these two vectors (see Figure 2).
Example.
\[\textbf{Three planes}\qquad\begin{align*} 2u+v+w=5\\\\ 4u-6v=-2\\\\ -2u+7v+2w=9 \end{align*}\]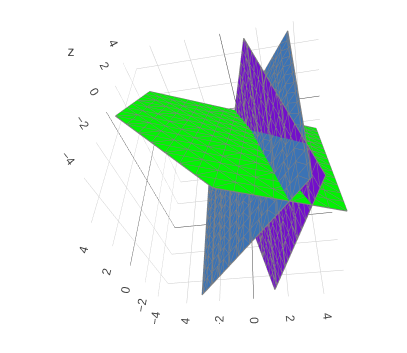
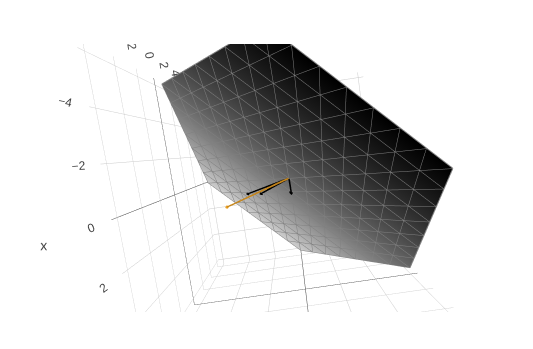
For three planes in general positions, they intersect at a point (Figure 3). The correspondent vector equation is
\[u\begin{bmatrix}2\\\\4\\\\-2\end{bmatrix}+v\begin{bmatrix}1\\\\-6\\\\7\end{bmatrix}+w\begin{bmatrix}1\\\\0\\\\2\end{bmatrix}=\begin{bmatrix}5\\\\-2\\\\9\end{bmatrix}.\]Similarly, we are seeking a combination of the three column vectors on the left-hand side that yields the column vector on the right-hand side (Figure 4).
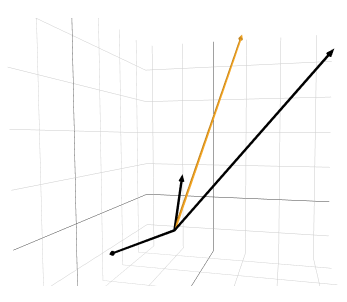
Remark. We use parentheses and commas for vectors written horizontally, e.g. $(1,2,3)$, and square brackets for vectors written vertically, e.g. $\begin{bmatrix}1\\2\\3\end{bmatrix}$.
Our ultimate aim is to extend our understanding beyond two or three dimensions into $n$ dimensions. In a system with $n$ equations and $n$ unknowns, the row picture illustrates the intersections of hyperplanes, while the column picture represents the linear combination of column vectors.
💡 Row picture: Intersection of planes Column picture: Combination of columns
The singular case
Row picture
In a singular linear equation system, if no solution exists, we say the equations are inconsistent. Otherwise, the planes might have a whole line in common or overlap entirely.
Column picture
The column picture of a singular case is more elegant. In this scenario, three column vectors must lie in a plane. (If they don’t, they can generate any vector in the space.) If the right-hand side column vector lies on the same plane, there are infinitely many solutions. Otherwise, the left-hand column vectors cannot generate the right-hand vector, indicating no solution exists.
Remark
| Nonsingular | Singular (infinitely many solutions) | Singular (no solution) | |
|---|---|---|---|
| Row | Has a point of intersection | Overlapping or has a common line | Has no intersection |
| Column | column vectors expand the entire space | column vectors lie on a plane, and the right-hand side column vector is on the plane | column vectors lie on a plane, and the right-hand side column vector is not on the plane |
undefined Example
Let’s consider
\[\begin{cases} x+y+z=2\\\\ 2x+3z=5\\\\ 3x+y+4z=6 \end{cases}\longleftrightarrow x\begin{bmatrix}1\\\\2\\\\3\end{bmatrix}+y\begin{bmatrix}1\\\\0\\\\1\end{bmatrix}+z\begin{bmatrix}1\\\\3\\\\4\end{bmatrix}=\begin{bmatrix}2\\\\5\\\\6\end{bmatrix}\]
Note that the zero vector $\begin{bmatrix}0\\0\\0\end{bmatrix}$ is a combination of the column vectors $\begin{bmatrix}1\\2\\3\end{bmatrix}$, $\begin{bmatrix}1\\0\\1\end{bmatrix}$, and $\begin{bmatrix}1\\3\\4\end{bmatrix}$. Allow me to directly writhe the solution
\[\begin{bmatrix}0\\\\0\\\\0\end{bmatrix} =3\begin{bmatrix}1\\\\2\\\\3\end{bmatrix} -\begin{bmatrix}1\\\\0\\\\1\end{bmatrix} -2\begin{bmatrix}1\\\\3\\\\4\end{bmatrix}.\]To solve this, we first observe that the second component of these column vectors yields the equation $3x-2z = 0$. This allows us to determine $x$ and $y$, and subsequently $z$.
How can we determine if three vectors lie in the same plane?
When three 3-dimensional vectors lie in the same plane, we can determine their coefficients by first assigning an arbitrary value to one variable, then solving for the second, and finally the third. However, this method becomes impractical for higher-dimensional spaces (vectors with many components) or when dealing with numerous vectors. A more efficient approach uses Gaussian elimination. We’ll introduce this method after covering Gaussian elimination and the concept of linear independence in our discussion of vector spaces.
Matrix Notation
A concise way to represent a linear equation system is to omit the variables and arrange the coefficients and right-hand sides in a matrix. This leaves us with the essential elements:
\[\begin{cases} \begin{array}{rcl} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n &= &b_1\\\\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n&=&b_2\\\\ \vdots&&\\\\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n&=&b_m \end{array} \end{cases} \quad\longleftrightarrow\quad \left[\begin{array}{c c c c | c } a_{11} & a_{12} & \cdots & a_{1n} & b_1\\\\ a_{21} & a_{22} & \cdots & a_{1n} & b_2\\\\ \vdots & \vdots & \ddots & \vdots & \vdots\\\\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m\\\\ \end{array}\right]\]From now on, we will represent linear equation systems in matrix form. You’ll need to translate between the matrix and equation forms yourself.
Gaussian Elimination
We will use several examples to demonstrate how Gaussian elimination works.
Example
Let’s examine the following linear equation system. We refer to the initial system as the original system.
\[\left[ \begin{array}{ccc|c} 2& 1 &1 &5\\\\ 4 &-6 &0 &-2\\\\ -2 &7 &2 &9 \end{array} \right] \qquad\textbf{The original system}\]In the original system, we refer to the term in the upper-left corner $a_{11}$ as the first pivot. Our initial task is to eliminate the numbers directly below this first pivot by adding or subtracting scaled versions of the first row from the subsequent rows.
\[\xrightarrow{\substack{(1)\times 2-(2)\to(2)\\\\(1)+(3)\to(3)}} \left[ \begin{array}{ccc|c} 2 & 1 & 1& 5\\\\ 0 & 8& 2& 12\\\\ 0 & 8& 3& 14 \end{array} \right]\qquad\textbf{an equivalent system}\]We refer to the new matrix as an equivalent system since both systems have the same solutions. The symbols above the long right arrow indicate the operations we’ve performed on the system. For example, “$(1) \times 2 - (2) \to (2)$” means we subtracted two times the first row from the second row and replaced the second row with the result. Similarly, “$(1)+(3)\to(3)$” means we add the first and the third row and replaced the third row with the result.
After completing this step, we shift our focus to the new pivot position at $a_{22}$, which we call the second pivot. We then repeat the process, eliminating the numbers directly below this second pivot.
\[\xrightarrow{-(2)+(3)\to(3)} \left[ \begin{array}{ccc|c} 2 & 1 & 1& 5\\\\ 0 & 8& 2& 12\\\\ 0 & 0& 1& 2 \end{array} \right]\qquad\textbf{the (lower) triangular system}\]When all entries below the diagonal (where $i > j$) are zero, we refer to this particular equivalent system as the (lower) triangular system. Once we achieve a triangular system, we can solve it by back-substitution.
\[\begin{split} \xrightarrow{-2\times(3)+(2)\to(2)} \left[ \begin{array}{ccc|c} 2 & 1 & 1& 5\\\\ 0 & 8& 0& 8\\\\ 0 & 0& 1& 2 \end{array} \right] \xrightarrow{(2)/8\to(2)} \left[ \begin{array}{ccc|c} 2 &1 &1 &5\\\\ 0 &1 &0 &1\\\\ 0 & 0 & 1&2 \end{array} \right]\\\\ \xrightarrow{(1)-(2)-(3)\to(1)} \left[ \begin{array}{ccc|c} 2 &0 &0 &2\\\\ 0 &1 &0 &1\\\\ 0 & 0 & 1&2 \end{array} \right] \xrightarrow{(1)/2\to(1)} \left[ \begin{array}{ccc|c} 1 &0 &0 &1\\\\ 0 &1 &0 &1\\\\ 0 & 0 & 1&2 \end{array} \right] \end{split}\]Thus, we conclude that $x=1$, $y=1$, and $z=2$.