PA=LU

If a permutation $P$ is necessary during the process of Gaussian elimination to obtain an upper triangular matrix, say

a strategy for decomposition is to move $P$ all the way to the right, adjacent to A. Let’s examine a few examples to illustrate how the strategy can be implemented.

Example. One can check the followings are true:

1. $P_{23}E_{13}=E_{12}P_{23}$

   \[\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 0 & 1\\\\ 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 1 & 0\\\\ c & 0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\\\ c & 1 & 0\\\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 0 & 1\\\\ 0 & 1 & 0 \end{bmatrix}\]

2. $P_{23}E_{12}=E_{13}P_{23}$

   \[\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 0 & 1\\\\ 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\\\ c & 1 & 0\\\\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 1 & 0\\\\ c & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 0 & 1\\\\ 0 & 1 & 0 \end{bmatrix}\]

3. $P_{13}E_{13}=E_{13}P_{13}$ (I didn’t show this example in class)

   \[\begin{bmatrix} 0 & 0 & 1\\\\ 0 & 1 & 0\\\\ 1 & 0 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0\\\\ 0 & 1 & 0\\\\ c & 0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & c\\\\ 0 & 1 & 0\\\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 0 & 0 & 1\\\\ 0 & 1 & 0\\\\ 1 & 0 & 0 \end{bmatrix}\]

Observing these matrices, we note that as we swap them, the indices of the elimination elementary matrices change correspondingly. More precisely, the permutation matrix $P_{ij}$ not only switches the $i$-th row and the $j$-th row but also permutes the integers $i$ to $j$ and $j$ to $i$. In general, we have the following proposition. However, before starting the proposition, let’s define some notations. Denote $(ij)$ as a function defined as

if $k\neq i$ or $j$. These notation can be pushed further. For example, $(123)$ is a function that maps $1$ to $2$, $2$ to $3$, and $3$ to $1$ with all other integers remaining fixed.

Proposition. We have $P_{ij}E_{i’j’}=E_{kl}P_{ij}$ where $k=(ij)i^\prime$ and $l=(ij)j^\prime$.

Remark. In class, we imposed conditions on indices to focus on cases essential for PA=LU decomposition. However, the proposition holds true even without these constraints.

Proof. The proof of this proposition employs a comprehensive examination of the following cases:

• Case 1: $j^\prime=i$ and $i^\prime\neq j$
• Case 2: $j^\prime=j$ and $i^\prime\neq i$
• Case 3: $i^\prime=i$ and $j^\prime\neq j$
• Case 4: $i^\prime=j$ and $j^\prime\neq i$
• Case 5: $i^\prime=i$ and $j^\prime=j$
• Case 6: $i^\prime=j$ and $j^\prime=i$
• Case 7: Neither $i^\prime$ nor $j^\prime$ is equal to $i$ or $j$.

Cases 1, 2, and 7 are the most relevant for our purposes and are effectively demonstrated by the examples provided earlier, except Case 7 which can be easily verified.

This proposition allows us to move a permutation matrix to the other side of an elimination elementary matrix. Furthermore, in a Gaussian elimination process, an elimination elementary matrix satisfies $i^\prime>i$, $j$, and $j^\prime$, so $E_{kl}$, the elimination elementary matrix after swapping, remains a valid elimination elementary matrix.

Summary

We can’t foresee whether a matrix $A$ can be PA=LU or A=LU decomposed before we actually perform the Gaussian elimination process. The process of these two decomposition is essentially the same except the middle step:

Step 1. Perform the Gaussian elimination process, and record the elementary matrices in every step.

Step 2. Apply the proposition to shift all permutation matrices to the right, resulting in the following expression:

Step 3. Multiply both sides by the inverses of $E_n$ to $E_1$ to obtain

Example. Find LU or PA=LU decomposition of the following matrix $A$

sol) The Gaussian elimination process is as the follows:

Therefore, we have

where $U$ is the last matrix in the above Gaussian elimination process. Now, we move the permutation matrix to the right. We need

and

Thus, we get

Consequently, the PA=LU decomposition of $A$ is

where $F_{12}^{-1}=E_{12}$, $F_{13}^{-1}=E_{13}$, and $D_3^{-1}=\text{diag}(1,1,-1)$.

Vector Space

When first introduced to vectors, we typically visualize them as arrows originating from the origin in a plane (two-dimensional space) or in space (three-dimensional space). This representation provides a vivid mental image of vectors. Vector operations, such as addition, can also be visualized—for instance, using the parallelogram law for vectors.

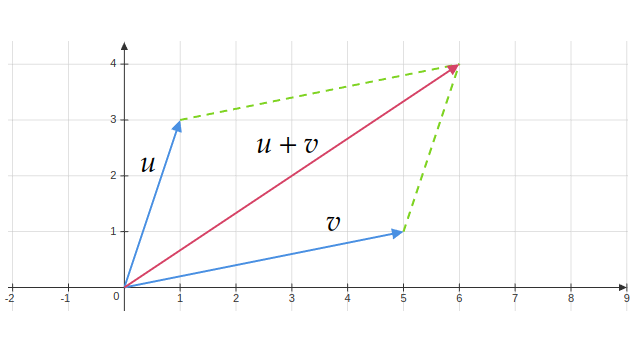
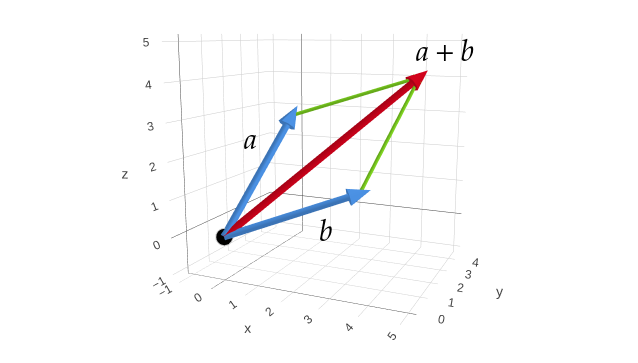
However, visualizing vector additions in higher-dimensional spaces is impractical. Nonetheless, we can easily represent a vector in higher dimensions algebraically. For example, the sum of two four-dimensional vectors $(a_1,a_2,a_3,a_4)$ and $(b_1,b_2,b_3,b_4)$ is simply the sum of their coordinates:

Even worse, we may encounter objects that share the same algebraic properties as vectors but don’t resemble vectors at all.

For example, solutions to a linear system $Ax = 0 $ can be considered vectors. If $v_1$ and $v_2$ are two solutions of the system, then any linear combination $c_1v_1+c_2v_2$ (where $c_1$ and $c_2$ are scalars) is a solution to the system. This property can be demonstrated as follows:

Here is an example of an object that doesn’t resemble a typical vector but shares the properties mentioned above. Consider solutions to the differential equation $y^{\prime\prime}+2y^{\prime}-3y=0$. We have two solutions: $f_1(x)=e^x$ and $f_2(x)=e^{-3x}$ (you can verify this by plugging these functions into the differential equation for $y$). Moreover, any linear combination $c_1f_1+c_2f_2$ are a solution to the differential equation because we have

Indeed, we see that a vector no longer resembles an arrow. This realization calls for an abstract, universal language to describe vectors.

English booster